Классическое кодирование информации
В компьютерных науках существует множество способов кодирования информации. Такие методы как код Хаффмана позволяют реконструировать исходную информацию после сжатия и поэтому называются сжатием без потерь.
В некоторых случаях, некоторым количеством данных можно пренебречь, зато получить большую степень сжатия. Думаю многие из вас знакомы с форматом JPEG, который обычно теряет некоторую часть информации от исходного растрового изображения. Алгоритм построен таким образом, что даже с некоторой потерей информации, изображение выглядит естественно и человеческий глаз обычно не улавливает такие изменения. Используя JPEG, можно уменьшить количество хранимой информации примерно в 10 раз, при этом качество изображения всё ещё останется высоким.
Использование нейронных сетей для хранения знаний
Даже используя современные методы хранения, всё-равно их нельзя назвать оптимальными по сравнению с тем, как хранит информацию человеческий мозг. Наш мозг не может похвастаться такой высокой точностью воспроизведения информации.
Однако он способен хранить взаимосвязи между объектами, из-за чего взглянув на изображение, мы можем не только распознать на ней объекты, что в нём существенно, а что второстепенно, но и соотнести полученную информацию с предыдущим опытом. Таким образом, вместо эффективного хранения сырых данных, необходимо хранить взаимосвязи, или же функции, которые в последствии можно повторно использовать. Искусственные нейронные сети, или же ориентированные графы, позволяют нам хранить данные в таком формате.
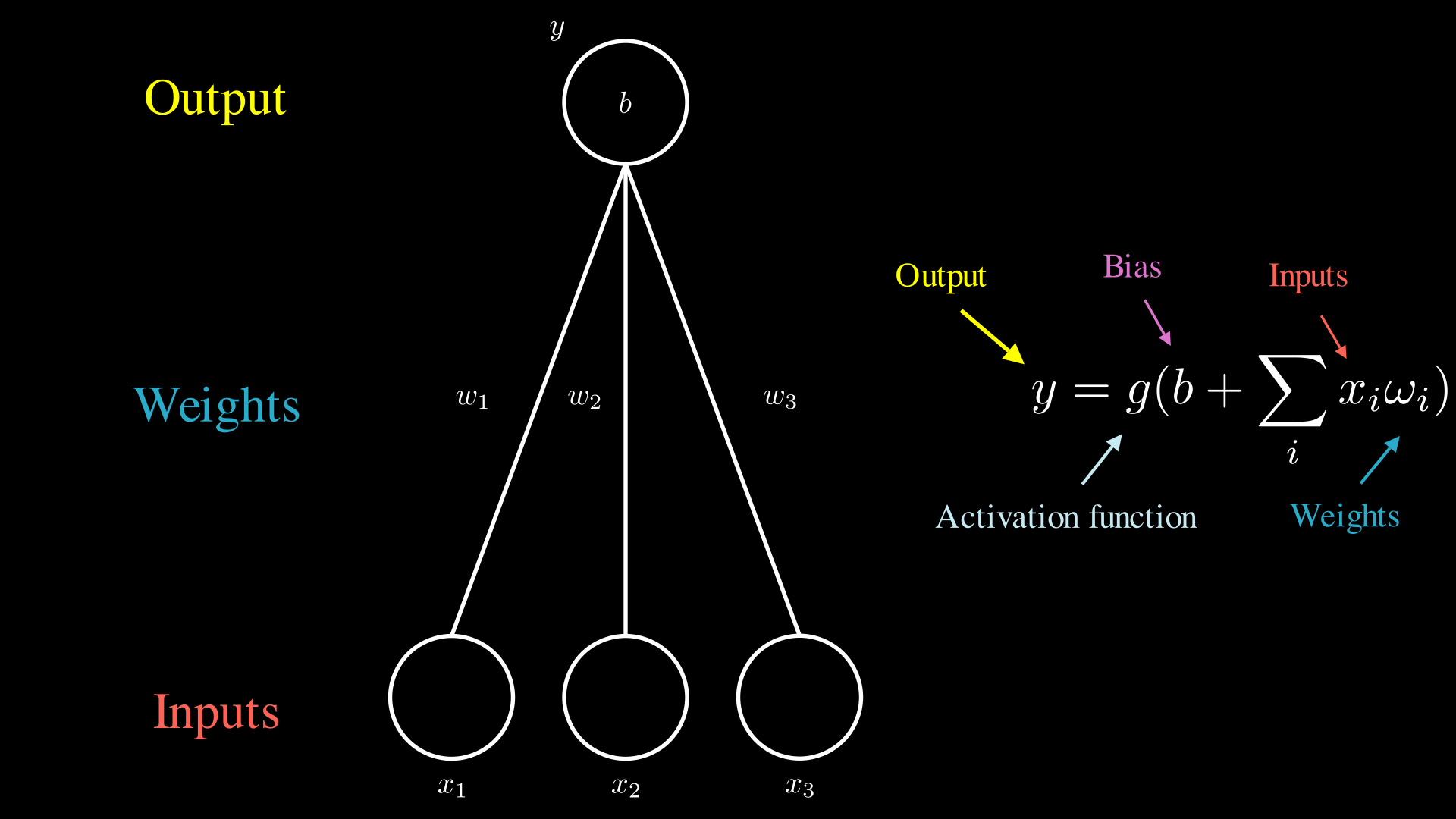
Искусственную нейронную сеть (далее просто нейронную сеть) можно изобразить следующим образом:
Устройство простого нейрона
где:
- x1, x2, x3 - узлы графа, которые являются входными данными. Обычно бинарное, натуральное или целое число;
- w1, w2, w3 - грани графа, или вес, которые показывают степень значимости параметров. Чем больше значение, тем больше узел влияет на конечный результат. Обычно рациональное число;
- y - узел графа, являющийся выходными данными. Обычно рациональное число;
- b - смещение, используется для балансировки сети. Значение может указываться как на узле сети, так и как отдельный входной параметр. Обычно рациональное число;
- g - функция активации. “Включает” и “выключает” узел сети, является нелинейной.
Принцип работы нейронной сети
Для начала рассмотрим простейший пример, который изображён выше. Вычисление выхода можно разбить на следующие шаги:
- Входные узлы принимают значение. Например 0 или 1;
- Все принятые значения перемножаются на соотвествующие веса, которые изображены на гранях;
- Далее все значения суммируются и к ним добавляется смещение b;
- Полученный результат подаётся в функцию активации, которая и определяет выходное значение.
Все приведённые шаги являются описанием простых математических операций, которые приведены справа. Конечно в реальных нейронных сетях вычисления не ведутся с каждым значением отдельно, а расчёты переводятся в векторный формат, который позволяет проводить те же математические операции более эффективно.
Данная сеть показывает принцип работы простейшего случая и на практике не используется. Обычно по такому же принципу сеть продолжается и узел “y”, наряду с другими такими же узлами, является входным аргументом для других узлов. В таком случае, узел “y” будет находится внутри нейронной сети и называется уже будет “скрытым элементом”, либо параметром сети. Именно о таких параметрах и говорят, когда называют размер сети в параметрах, поскольку в них уже можно кодировать уже какие-либо знания.
Многослойный перцептрон
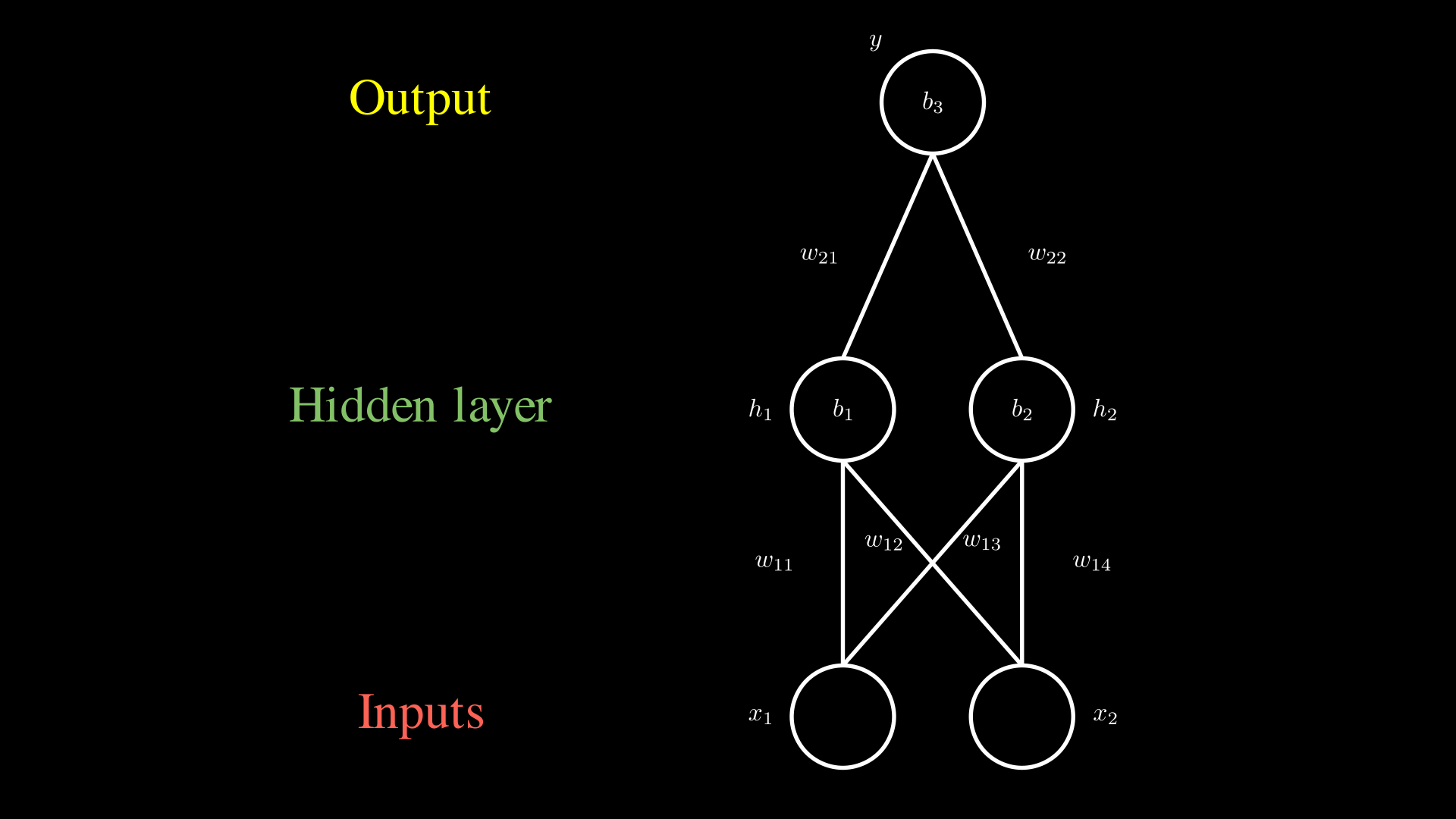
Одним из простейших примеров “рабочей” нейронной сети может служить многослойный перцептрон, который показан ниже.
Однослойный перцептрон
В данной сети можно выделить 3 слоя: входной (input), скрытый (hidden) и выходной (output). Алгоритм работы данной сети идентичен шагам описанным выше, с той лишь разницей, что шаги выполняются для каждого узла скрытого слоя, а затем алгоритм повторяется для выходного узла.
Функция активации
Чтобы внести ясность в рассуждения, прежде чем посмотреть применение сети на практике, стоит остановиться на функциях активации. Данные функции активируют нейроны сети, таким образом “включая” или “выключая” их из расчётов сети, либо усиливают или ослабляют их влияние на конечный результат.
Функции активации можно разделить на линейные и нелинейные. Первые обычно не используются в нейронных сетях, поскольку Джордж Цыбенко в 1989 году доказал, что любую нейронную сеть с прямой связью (feed-forward), в которой так же отсутствуют внутренние циклы, можно аппроксимировать (упростить) до сети с одним скрытым слоем. Данный факт ограничивает размер и архитектуру нейронных сетей, что не позволяет делать сети поистине “глубокими”, то есть иметь множество внутренних слоёв.
Эту проблему решает использование нелинейных функций активации, позволяя увеличивать размер сети и описывать более сложные структуры данных. Самые распространённые нелинейные функции активации следующие:
Шаговая функция
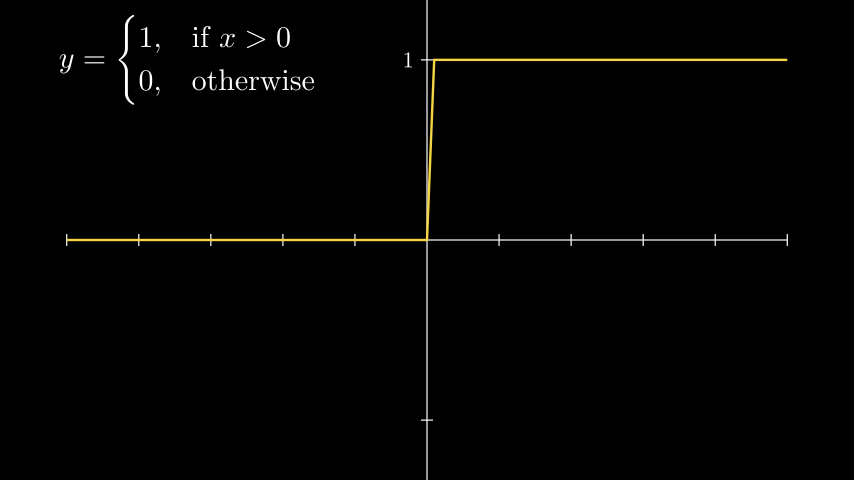Heaviside (step function). Хевисайд (шаговая) функция.
Самая простая нелинейная функция, которая имеет лишь два значения: 0, 1. В дальшейших примерах будем ипользовать именно эту функцию.
Сигмоидная функция
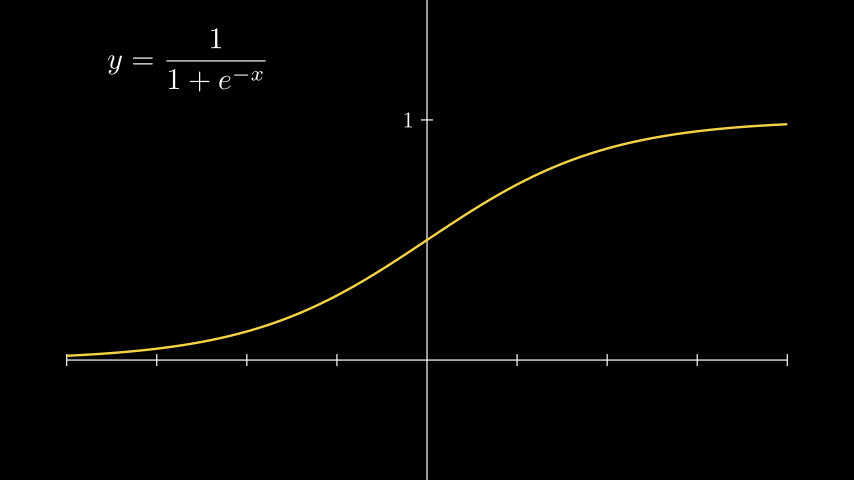
Сигмоидная функция
Одна из первых функций активации. Ранее имела широкую популярность из-за относительной простоты, и то, что интервал выходных значений находится в пределях [0, 1]. Благодаря этому, выходные значения функции можно напрямую использовать в вероятностных моделях, без дальнейшей нормализации и регуляризации.
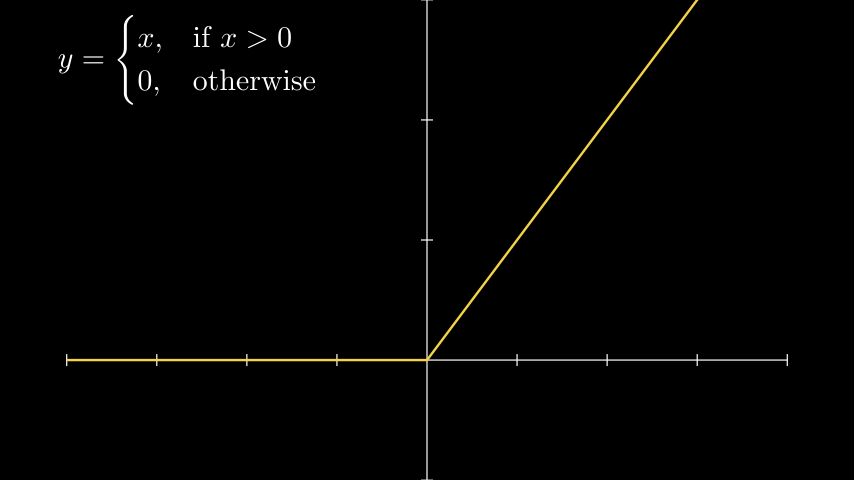
ReLU (Rectified Linear Unit)
ReLU
До сих пор функция ReLU применяется очень широко и является одной из самых популярных. Всё дело в том, что сходимость нейронной сети при использовании ReLU происходила гораздо быстрее, в сравнении с сигмоидой и тангенциальной функцией. При этом, вычислять результат данной функции стало ещё проще.
GELU (Gaussian Error Linear Unit)
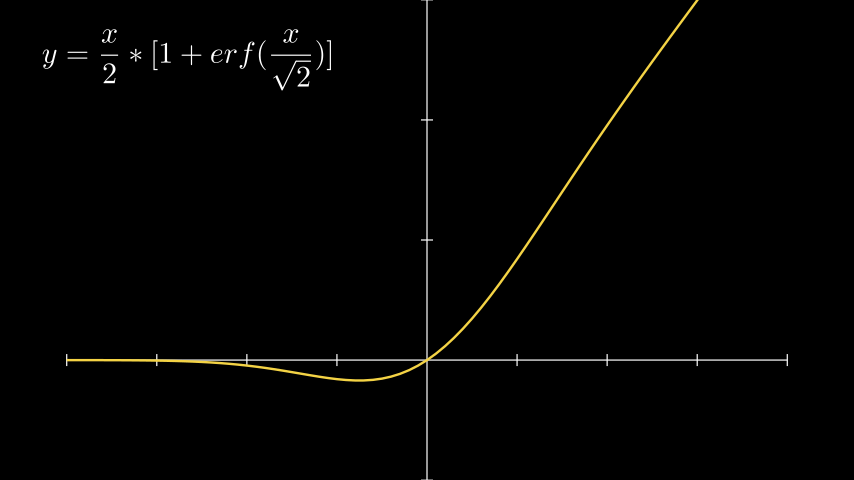GELU Нет, эта функция не имеет ничего общего с героем Джелу из серии игр “Меча и магии”. Функция активации GELU очень похожа на ReLU, с той лишь разницей, что переход от отрицательных, к положительным значениям является более плавный. При положительных значениях, GELU лишь асимптотически приближается к ReLU и не является линейной, в отличии от последней функции. Всё это способствует более быстрому схождению нейронной сети во время обучения.
Функции активации на практике
Для примера возьмём некие данные, которые можно отобразить на координатной плоскости.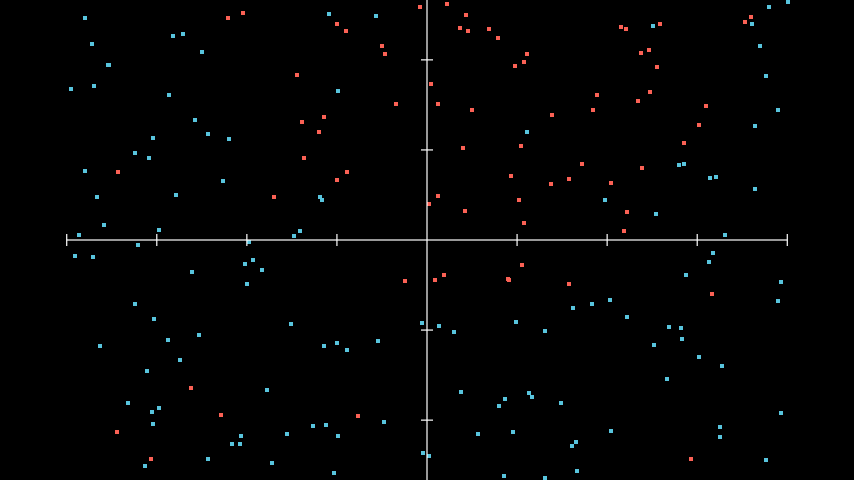 
Пример данных для их классификации
Нейронная сеть должна научиться классифицировать данные из этого набора. С первого взгляда можно предположить, что линейная модель не способна достаточно точно разделить данный набор на два класса. Попробуем использовать линейную функцию активации для данного набора данных.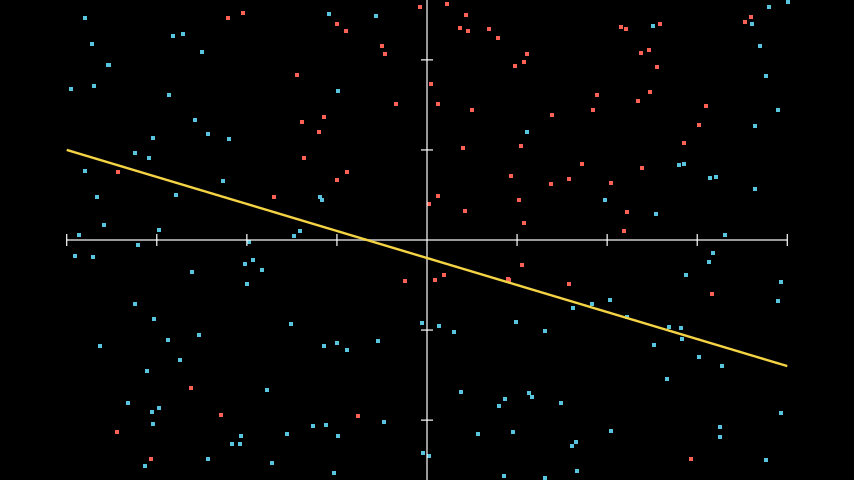 
Применение линейной функции для решения нелинейных задач
Как видно, большую часть точек всё же удалось правильно разделить и классифицировать. Но большая часть экземпляров были неправильно определены, из-за того, что наша функция слишком простая.
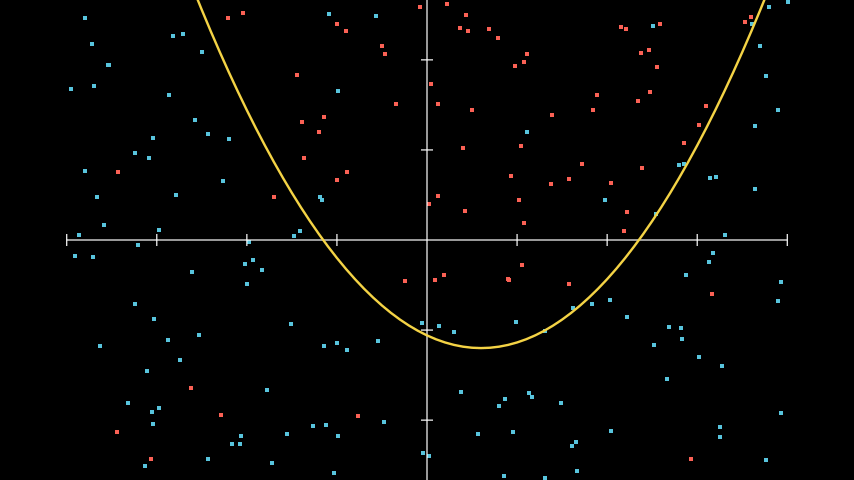Применение нелинейной функции для решения нелинейных задач
При использовании нелинейности, мы можем более точно провести границу между двумя классами. Это так же возволяет сделать модели которые мы используем с большим количеством параметров, что позволяем нам описывать более сложные данные.
XOR
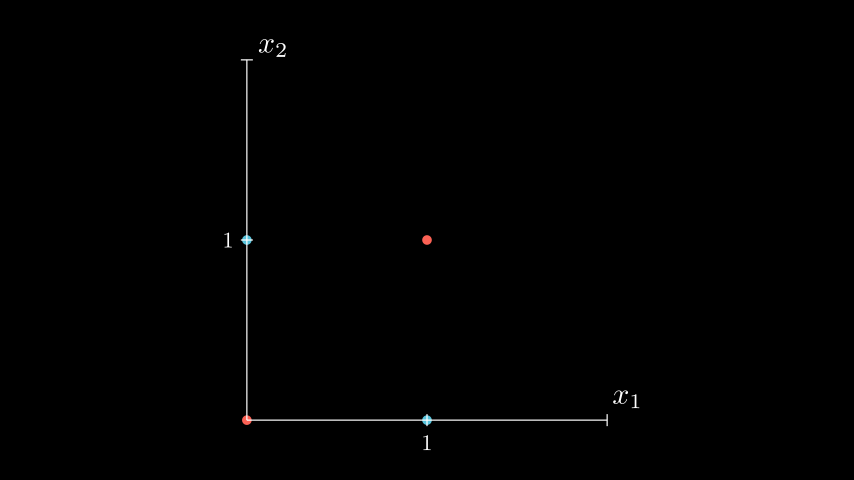
Рассмотрим применение простой нейронной сети, которая сможет выполнять функцию XOR (исключающий OR). Все возможные значения аргументов и их результат можно изобразить в следующей таблице:
| x1 | x2 | y |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Как известно, функция XOR не является линейно разделимой. Это значит, что невозможно провести одну прямую, которая разделит все точки так, что с одной стороны будут находится красные точки, а с другой синие.
(Конечно не стоит верить мне наслово. Желающие могут попробовать доказать/опровергнуть это в качестве домашнего задания.)
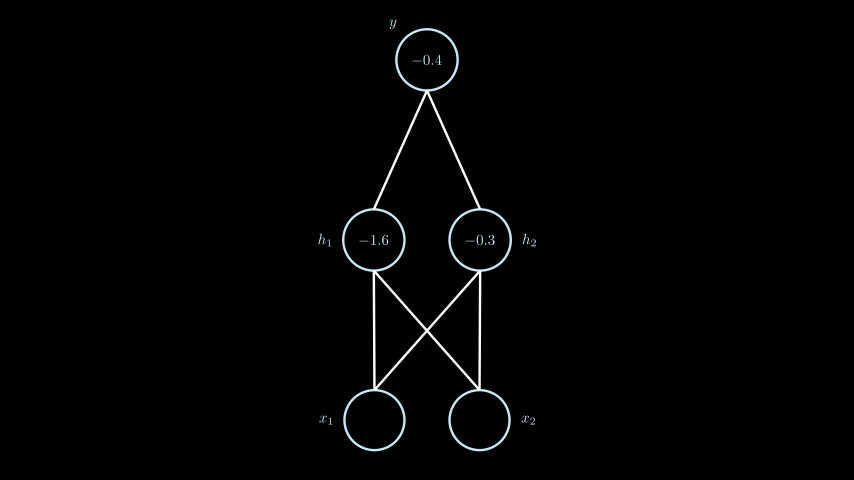
Для решения этой задачи используем многослойный перцептрон, с такой же структурой, как показан выше. В этот раз используем реальные значения.
В качестве функции активации будем использовать простейшую Шаговую функцию. Результат функции отображается либо зелёным, при значении “1”, либо красным, когда значение равно “0”.
В целях упрощения, в данном примере все вычисления происходят последовательно для каждого слоя сети и каждого узла в отдельности. Когда весь слой сети расчитан, его результат подаётся на следующий уровень, пока не дойдёт до выходного слоя y. Обычно для более быстрого расчёта вычисления происходят в векторной форме.
Заключение
В статье описан алгоритм работы простейшего многослойного перцептрона и показан пример его использования в качестве XOR функции.
В следующих статьях рассмотрим алгоритм градиентного спуска, благодаря которому можно обучить нейронную сеть. Так же рассмотрим методы оптимизации и реализуем алгоритм обучения на практике.